Board problem: Using the same method as for 4.3/12, find a closed formula for f(n)=12+22+...+n2. You will not get any credit if you just prove the formula by induction.
Bonus problem: Using the same method as for 4.3/12, find a closed formula for f(n)=13+23+...+n3. (B07, 10 points)
Bonus: Using the generating function method to count the triangulations of a regular polygon (on pages 148 and 149) as a guide, transform the recurrence for the Catalan numbers in our handout into a quadratic equation, solve it, and derive the closed form formula for the Catalan numbers. (B06, 10 points)
Bonus: 3.5/3 (B05, 5 points).
Board problem:
- The sequence a0, a1, a2,...
is given by the initial conditions a0=1
, a1=4 and by the
recurrence an+2=4 ·
an+1-4 · an.
Using the method shown in class, find a closed form formula for an.
Board problems:
- Using the inclusion-exclusion formula, find the number of ternary strings of length 5 that have no two consecutive 1's.
- The sequence a0, a1, a2,...
is given by the initial conditions a0=3
, a1=5 and by the
recurrence an+2=4 ·
an+1-3 · an.
Prove by induction that an=2+3n.
- 3.1/5a (B03, 5 points)
- 3.2/9b (B04, 5 points)
Bonus: Using algebra, prove Pascal's formula
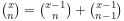 in the case when x is not
necessarily an integer (B05, 3 points).
in the case when x is not
necessarily an integer (B05, 3 points).
Bonus: Extend Vandermonde's formula (formula (2.5) in section 2.1) to the case when m and n are not integers, and are replaced with variables x and y respectively. (B02, 10 points, you may want to use that a nonzero polynomial in one variable has only finitely many roots).
Bonus question: 1.1/12 (B01, 5 points, you must assume each set is represented by a circle).