Bonus: Using the statement in the previous bonus question, find the eigenvalues of the (3-dimensional) cube.
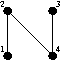 |
and | 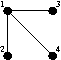 |
for K4, | |
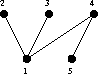
|
for K2,3. (One part is {1,5} the other is {2,3,4}.) | |||
Bonus: Denote the incidence matrix of a graph by B (the columns are indexed by the edges) and its transpose by BT. Prove that BBT differs from the adjacency matrix only on its diagonal, and describe the difference.
No new hw assigned on Friday. Review for the next test will be on Monday, but I already distributed a Sample Test 2.
- Find the dual of the graph shown in the picture:
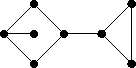
- Prove that in a self-dual planar graph there is at least one vertex of degree 3.
From the book: 12.1.2, 12.1.3, 12.1.5 (i) and (ii), 12.1.6.
Bonus: 1.2.1.5 (iii)
Draw a map of six (disconnected) countries that can not be colored with less than six colors. For even more bonus points, explain how to draw a map of n countries that can not be colored with less than n colors.
Bonus: Prove that the edge graph of an n-dimensional hypercube is bipartite.
Bonus: Assume T and T' are trees on the same vertex set, with edge sets {e1, e2, ..., ev-1} and {f1, f2, ..., fv-1}, respectively. Assume that e1=f1, e2=f2, ..., ei-1=fi-1 but ei is not an edge of T'. We know that then ei, together with some edges fi1, fi2, ..., fikfrom T', forms a cycle. Prove that at least fij may be added to {e1, e2, ...,ei-1} without forming a cycle.
No new was homework assigned on Friday Sep 23. Remember the test on Monday. If you missed the class on Friday, download the Sample Test 1 I distributed.
To complete the proof of Theorem 3.5, prove the following:
Lemma: Assume the positive integers x, y and v satisfy x+y=v. Prove that then xy is greater than or equal to v-1.
Bonus: Prove that (iii) implies (iv) in Theorem 3.3.
Note: In Exercise 2.2.3 (ii), the weight of the edge sc is missing. Assume it is 10.
Bonus: 1.1.7; describe the adjacency matrix of the Cartesian product of two graphs.